Frank Duckworth dies: How his DLS method works

Here is why the method was brought in, and how it works (in simple terms).

‘Fair results in foul weather’

In 1992, Duckworth presented a paper, “A fair result in foul weather” at the Royal Statistical Society. This was a response to the rather farcical ending of the 1992 South Africa vs England semi final. South Africa needed an achievable 22 from 13 balls when rain interrupted play. After the rain delay, the revised target was calculated as 22 required of one ball — an impossible task.

The revised target was determined using the newly adopted Most Productive Overs method. Devised by a panel of cricketing experts, the method took into account runs scored in the best ‘x’ number of overs in the first innings to set the target, when ‘x’ was the number of overs the second innings was reduced to. So if a team scored 300 runs in 50 overs, and 200 of these came in say 25 overs, a match reduced to 25 overs would set a target of 201 for the chasing team.

While the MPO method took into account that run scoring is not evenly distributed across the innings, something that a simple average run rate calculation does not, it unfairly penalised the chasing team by simply ignoring the best overs bowled by them in its calculations of a revised target. It also took no consideration of how wickets impacted run-scoring.

Duckworth said in an interview in 2007: “[Watching the 1992 semi final] I realised that it was a mathematical problem that required a mathematical solution”. He presented his idea for an alternative at the RSS, following which Lewis got in touch.

The DLS method

The DL method introduced the concept of ‘resources’ in making score estimations for truncated games. In limited-overs cricket, each team, in effect, has two ‘resources’ to score as many runs as possible — the number of overs (balls) yet to be bowled, and the number of wickets in hand. Duckworth and Lewis studied historical scores and found that there is a very close correlation between availability of these resources and a team’s final score.

In simple words, the more balls left to be bowled, the more a team can score. Similarly, the more the wickets in hand, the more it can score. As Duckworth and Lewis wrote in their 1997 paper: “Clearly, a team with 20 overs to bat with all ten wickets in hand has a greater run scoring potential than a team that has lost, say, eight wickets” (“A fair method for resetting the target in interrupted one-day cricket matches”).

The DL method converts all possible combinations of balls and wickets in hand to a combined “resources remaining” figure, which is expressed in percentage — full 50 overs, and 10 wickets in hand means 100% resources available.

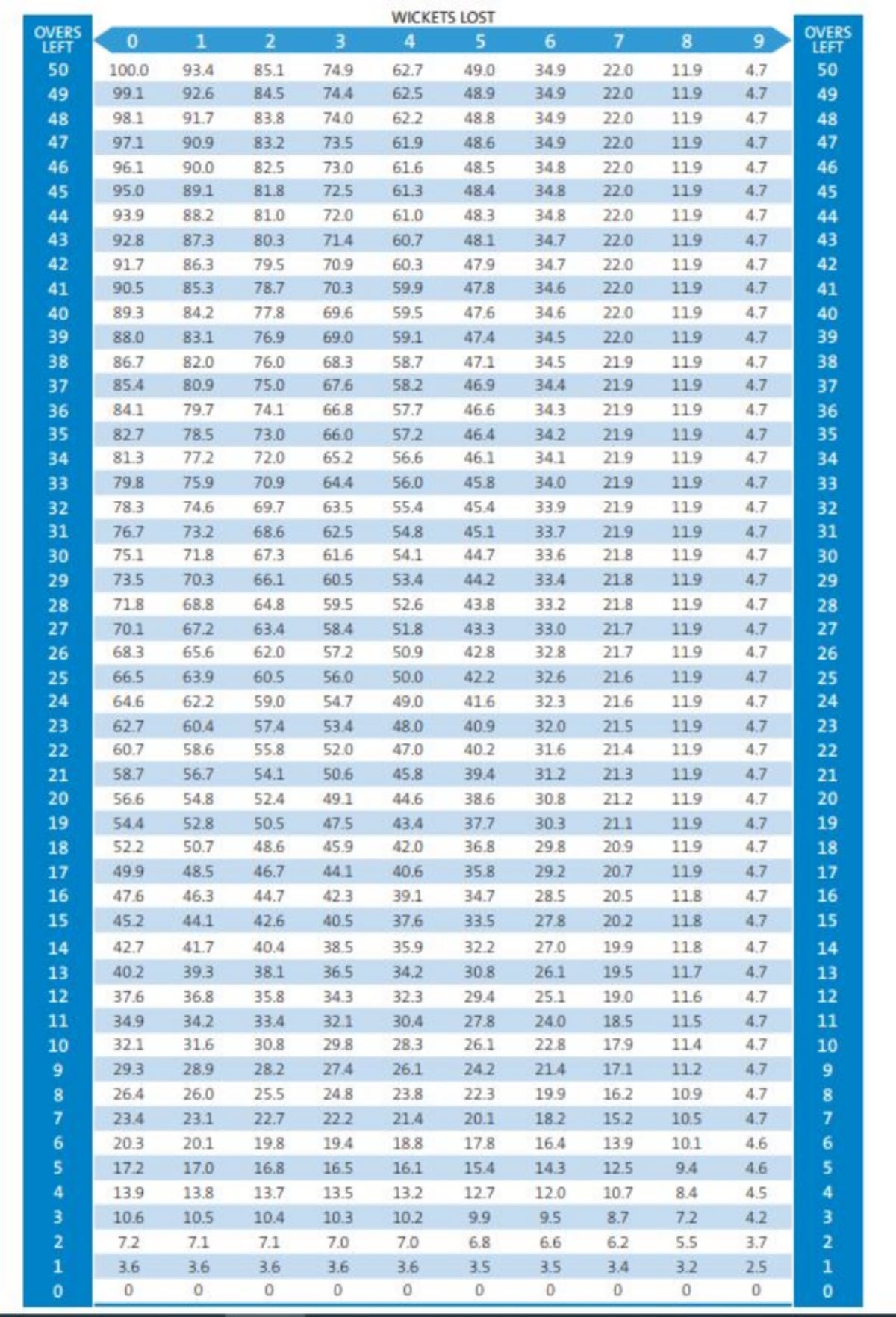Table of resource percentages remaining – over by over, DLS Standard Edition (ICC)

Target scores for a team batting second can be adjusted (either up or down) from the total of the team batting first, simply based on the number of resources either team has lost. The following formula is used:

Team 2’s par score = Team 1’s actual score x Team 2’s resources/Team 1’s resources

The true achievement of Duckworth and Lewis was calculating the proportion between total runs that can be scored, and the resources remaining (both runs and balls). While the extremes are intuitively arrived at (100% at the beginning, 0% at the end), how each over and wicket impacts the game state was determined using a lot of number-crunching, and some statistical sorcery which is beyond the scope of this article.

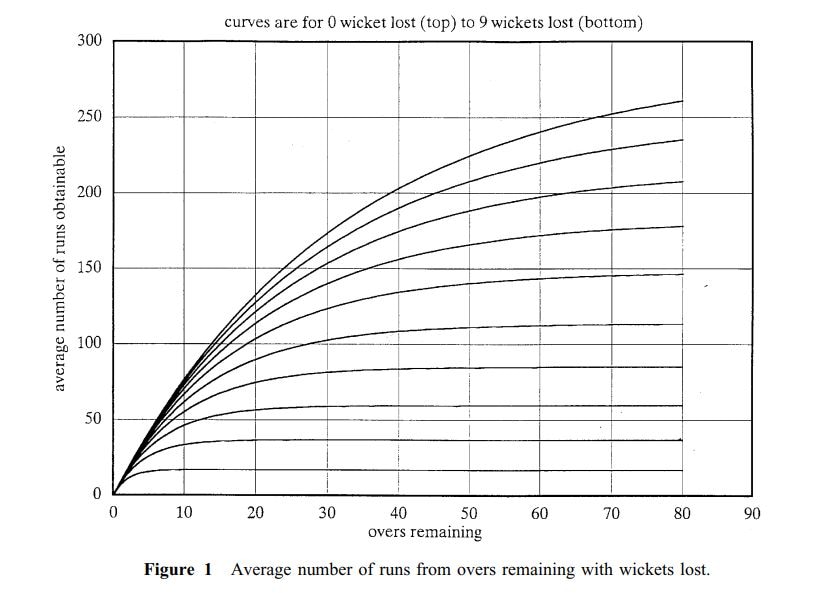Average number of runs from overs remaining with wickets lost. (Duckworth and Lewis)

“Commercial confidentiality prevents the disclosure of the mathematical definitions of these functions. They have been obtained following extensive research and experimentation so that… they behave as expected under various practical situations and give sensible results,” Duckworth and Lewis wrote.

Some criticisms

The DLS method has faced criticism on the grounds that it weighs wickets more heavily (as a resource) than balls available. This means that in big run chases with rain looming, teams simply need to keep wickets in hand to match the DLS par score — they can win even while scoring at a losing rate. The underlying assumption of “keeping wickets in hand” is in line with traditional cricketing logic, but flies in the face of data today, especially as run-scoring has become ever more rampant.

This emphasis on wickets has also meant that the DLS is less accurate for T20s, where one good partnership can decisively swing a game. Take for instance this year’s IPL winners KKR, who boasted a batting line-up with solid hitting at number 8, sometimes even at number 9. While traditionally a team may struggle to score at a fast rate after losing five or six wickets, that was definitely not the case with KKR.

Steven Stern’s additions to the DL method updated it for the modern-day run-environment, but these criticisms still persist. Today, the data to calculate the DLS par score is taken from a running average of four years of international cricket.